对称性展现数学之美！杨振宁是如何为粒子物理奠基的(杨振宁 宇宙对称)

对称性展现数学之美！杨振宁是如何为粒子物理奠基的， 贝尔原本想通过自己的贝尔不等式推翻玻尔对EPR思想实验的量子解释。可谁曾料到，实验真的做了之后，结果居然是一记耳光。本来是要输出一波的，结果给了对方一个头。对此，泊松打电话给专家。

有些朋友还不明白贝尔不等式怎么能检验隐变量是否存在。其实如果你仔细了解这个不等式的推导过程。你知道，因为它的本质是来源于逻辑的。就核心本质而言，与理论本身关系不大。

事实上，在这一点上，我们几乎已经介绍了量子力学的早期基础部分。我之前介绍的几乎都是关于20世纪上半叶的。接下来，我将介绍一些自20世纪50年代以来离我们并不遥远的发展。

量子理论的下半场，下垂的果实越来越少，颠覆性的突破不再那么容易出现。如果说前半部分是开拓，那么后半部分主要是打基础和盖楼。后半段出现的名词已经不像量子纠缠了。

量子理解是如此的直白和熟悉。

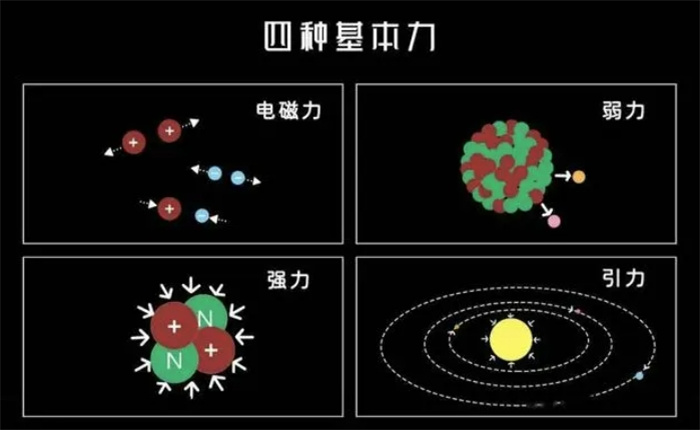
例如，今天要讨论的杨-米尔斯理论。从牛顿的经典力学到爱因斯坦的广义相对论，在四种基本力中，引力最先被我们认识。此后，理论成功描述的第二个基本力是电磁力。

更早的时候，麦克斯韦率先通过一组简洁优美的方程组统一了电和磁。这个著名的麦克斯韦方程组体现了电磁学的一个重要特征——电荷守恒。如果某处突然出现负电荷，

那么另一个地方一定有相应的正电荷。

早期的电磁学可以说是基于自然现象，主要来源于物理学中的实验。但是后来，德国数学家赫尔曼韦尔基于电荷守恒的局域对称性，通过他自己的规范场理论，

从数学上直接推导出与麦克斯韦方程组等价的电磁方程。

在泡利的推动下，这个第一个规范场理论在物理学中传播开来。规范理论中的规范不变性完美展现了物理学中的数学之美。这种数学对称的美妙之处。这时，它也吸引了另一个年轻人，他就是杨振宁。

事实上，当杨振宁在国立西南联合大学读书时，他就已经有了规场的想法。后来我在芝加哥大学读研究生的时候，也在这方面做了一些尝试。后来，1950年，杨振宁博士毕业，在普林斯顿高等研究院工作。

后来，他去布鲁克海文国家实验室做了一段时间的访问学者。

当时，布鲁克海文实验室拥有世界上最大的粒子加速器。此时正是粒子物理的大爆发时期，各种新粒子不断被发现。随着越来越多新粒子的出现，原有动力学方程中的计算项越来越多，整个过程变得异常复杂。

对于这类问题，通常的做法是等到积累了足够多的实验数据后再考虑如何解决。但是这时，杨振宁已经意识到，是时候用一种新的理论来描述这些粒子之间的相互作用了。

对称的概念可能在其中再次发挥作用。

所以他决定从原子核内的强相互作用入手。我们知道，在原子核中，除了中性中子，质子都带正电。那么不同的质子应该互相排斥，因为它们携带相同的电荷。为什么他们在现实中被牢牢捆绑在一起？

是的，主要是因为它们之间存在着比电磁相互作用更强的相互作用。没错，这就是在三体结构中建造水滴壳所需的力度。类似于电磁相互作用中的电荷守恒，

在强相互作用中还有一个守恒——同位旋守恒。

注意，同位旋不是自旋，不是角动量的单位，是一个无量纲的物理量。既然电荷守恒可以推导出电磁相互作用，那么同位旋守恒可以推导出强相互作用吗？

这时，与杨振宁在同一办公室的米尔斯博士也对这个问题产生了兴趣。最后他们解决了这个问题，连续发表了两篇论文。今天，粒子标准模型的基础——杨-米尔斯规范场理论已经形成。

但是，在文章的最后，他们提到了理论中还有一个未解决的问题。根据他们的理论，有这样一种情况，一个场对应的规范粒子的质量出现了，不应该是零而是零。当杨振宁谈到第一个公式时，

保利一针见血。你的领域相应的质量如何？

杨振宁顿时出了一身冷汗，只能支支吾吾地说，我不知道，这个问题比较复杂。我们也研究过，但没有明确的结论。显然泡利对他的回答并不满意，场面一度变得十分尴尬。泡利实际上考虑把规范场扩展到强相互作用的问题。

并且意识到有一个质量问题很难解决。

那么，既然有问题，为什么杨振宁等人坚持发表论文呢？首先，勇气是必不可少的，但杨振宁的勇气很大程度上来自于他对美的自信和坚持。由于对细节的执念，数学之美显然没有被泡利完全理解。

他更关注身体问题。

杨振宁一直对数学美情有独钟。对于如此美丽的数学结构，他认为自然界应该是这样的。至于粒子的质量，在数学之美面前，已经变得不那么重要了。这个小问题应该是暂时的，以后会解决的。

但物理终究是物理，再美的理论也要解决问题。当时人们认为杨-米尔斯理论只是一个数学结构，可能对物理学有影响。虽然结构本身简单美观，但并没有太多的物理意义。

因此，物理学界对这一新理论的关注并不长久。虽然杨-米尔斯理论最初被忽略，但它的非阿贝尔规范场模型为所有已知甚至未知的粒子提供了统一的框架。

为以后的粒子物理学奠定了基础。

后来不仅强相互作用，电弱统一和粒子标准模型都将建立在这个理论框架上。如今，对称性主导了相互作用，这甚至成为了理论物理学家的坚定信念。扬-米尔斯理论蕴含着巨大的能量。随着粒子物理学的发展，

它的能量会逐渐释放。

对称性展现数学之美！杨振宁是如何为粒子物理奠基的，以上就是本文为您收集整理的对称性展现数学之美！杨振宁是如何为粒子物理奠基的最新内容，希望能帮到您！更多相关内容欢迎关注。